Änderung Anhang PAngV vom 11.06.2010

Anhang PAngV a.F. (alte Fassung)
in der vor dem 11.06.2010 geltenden Fassung

Anhang PAngV n.F. (neue Fassung)
in der am 11.06.2010 geltenden Fassung
durch Artikel 6 G. v. 29.07.2009 BGBl. I S. 2355

(Text alte Fassung)

Anhang (zu § 6)

1. Die mathematische Formel zur Berechnung des Vomhundertsatzes gemäß § 6 Abs. 1 lautet: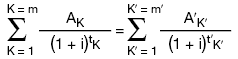

Diese drückt die Gleichheit zwischen Darlehen einerseits und Tilgungszahlungen und Kosten andererseits aus.

Hierbei ist:

K Die laufende Nummer der Auszahlung eines Darlehens oder Darlehensabschnitts

K´ Die laufende Nummer einer Tilgungszahlung oder einer Zahlung von Kosten

A_K Der Auszahlungsbetrag des Darlehens mit der Nummer K

A´_K´ Der Betrag der Tilgungszahlung oder einer Zahlung von Kosten mit der Nummer K´

Σ Das Summationszeichen

m Die laufende Nummer der letzten Auszahlung des Darlehens oder Darlehensabschnitts

m´ Die laufende Nummer der letzten Tilgungszahlung oder der letzten Zahlung der Kosten

t_K Der in Jahren oder Jahresbruchteilen ausgedrückte Zeitabstand zwischen dem Zeitpunkt der Darlehensauszahlung mit der Nummer 1 und den Zeitpunkten darauf folgender Darlehensauszahlungen mit den Nummern 2 bis m; t₁ = 0

t´_K´ Der in Jahren oder Jahresbruchteilen ausgedrückte Zeitabstand zwischen dem Zeitpunkt der Darlehensauszahlung mit der Nummer 1 und den Zeitpunkten der Tilgungszahlung oder Zahlungen von Kosten mit den Nummern 1 bis m´

i Der effektive Zinssatz, der entweder algebraisch oder durch schrittweise Annäherungen oder durch ein Computerprogramm errechnet werden kann, wenn die sonstigen Gleichungsgrößen aus dem Vertrag oder auf andere Weise bekannt sind.

2. Die von Kreditgeber und Kreditnehmer zu unterschiedlichen Zeitpunkten gezahlten Beträge sind nicht notwendigerweise gleich groß und werden nicht notwendigerweise in gleichen Zeitabständen entrichtet.

3. Anfangszeitpunkt ist der Tag der ersten Darlehensauszahlung.

4. Die Spannen t_K und t´_K´ werden in Jahren oder Jahresbruchteilen ausgedrückt. Zugrunde gelegt werden für das Jahr 365 Tage, 52 Wochen oder 12 gleichlange Monate, wobei für letztere eine Länge von 365/12 Tagen = 30,41 6 Tagen angenommen wird.

5. Der Vomhundertsatz ist auf zwei Dezimalstellen genau anzugeben. Bei der Rundung ist folgende Regel anzuwenden:

Ist die Ziffer der Dezimalstelle, die auf die zweite Dezimalstelle folgt, größer als oder gleich 5, so erhöht sich die Ziffer der betreffenden Dezimalstelle um eine Einheit.

6. Die Berechnung des Vomhundertsatzes hat zu einem Ergebnis gleicher Art wie bei den folgenden Beispielen zu führen:

6.1

Die Darlehenssumme S beträgt 1.000 Euro.

Diese Summe wird 1,5 Jahre (d. h. 1,5 x 365 = 547,5 Tage, 1,5 x 12 = 18 Monate oder 1,5 x 52 = 78 Wochen) nach Darlehensauszahlung, in einer einzigen Zahlung in Höhe von 1.200 Euro zurückgezahlt.

Daraus ergibt sich folgende Gleichung: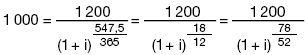

oder

(1+i)^1,5 = 1,2
1+i = 1,12924 ...
i = 0,12924 ...

Der Betrag wird auf 12,92 % gerundet.

6.2

Die Darlehenssumme S beträgt 1.000 Euro, jedoch behält der Darlehensgeber 50 Euro für Kreditwürdigkeitsprüfungs- und Bearbeitungskosten ein, so dass sich der Auszahlungsbetrag des Darlehens auf 950 Euro beläuft. Die Rückzahlung der 1.200 Euro erfolgt wie im ersten Beispiel 1,5 Jahre nach der Darlehensauszahlung.

Daraus ergibt sich folgende Gleichung: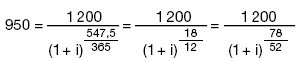

oder

(1+i)^1,5 = 1.200/950 = 1,26315 ...
1+i = 1,16852 ...
i = 0,16852 ...

Dieses Ergebnis wird auf 16,85 % gerundet.

6.3

Die Darlehenssumme S beträgt 1.000 Euro, die in zwei Raten von jeweils 600 Euro nach einem bzw. nach zwei Jahren rückzahlbar ist.

Daraus ergibt sich folgende Gleichung: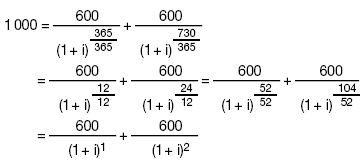

Die Gleichung wird algebraisch gelöst und ergibt i = 0,13066 ...; dieses Ergebnis wird auf 13,07 % gerundet.

6.4

Die Darlehenssumme S beträgt 1.000 Euro. Der Darlehensnehmer hat folgende Raten zurückzuzahlen:


Nach 3 Monaten
(0,25 Jahre/13 Wochen/91,25 Tage) | 272 Euro

Nach 6 Monaten
(0,5 Jahre/26 Wochen/182,5 Tage) | 272 Euro

Nach 12 Monaten
(1 Jahr/52 Wochen/365 Tage) | 544 Euro

Insgesamt | 1.088 Euro.


Daraus ergibt sich folgende Gleichung:

Mit dieser Gleichung lässt sich i durch schrittweise Annäherungen errechnen, die auf einem Taschenrechner programmiert werden können.

Das Ergebnis lautet i = 0,13185 ...; dieses Ergebnis wird auf 13,19 % gerundet.

6.5

Die Darlehenssumme S beträgt 4.000 Euro, jedoch behält der Darlehensgeber 80 Euro für Kreditwürdigkeitsprüfungs- und Bearbeitungskosten ein, so dass sich der Auszahlungsbetrag des Darlehens auf 3.920 Euro beläuft. Die Darlehensauszahlung erfolgt am 28. Februar 2000. Der Darlehensnehmer hat folgende Raten zurückzuzahlen:


• Am 30. März 2000 | 30,00 Euro,

• Am 30. März 2001 | 1360,00 Euro,

• Am 30. März 2002 | 1270,00 Euro,

• Am 30. März 2003 | 1.180,00 Euro,

• Am 28. Februar 2004 | 1.082,50 Euro.

• Insgesamt | 4.922,50 Euro.


Daraus ergibt sich folgende Gleichung: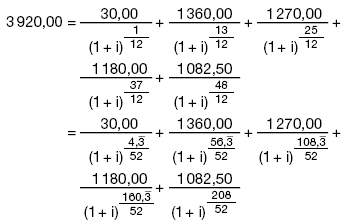

Mit dieser Gleichung lässt sich i durch schrittweise Annäherungen errechnen, die auf einem Taschenrechner programmiert werden können.

Das Ergebnis lautet i = 0,09958 ...; dieses Ergebnis wird auf 9,96 % gerundet.

6.6

Die Darlehenssumme S beträgt 10 000 Euro und die Darlehensauszahlung erfolgt am 15. Oktober 1999. Der Darlehensnehmer hat folgende Raten zurückzuzahlen:


• Jeweils am 15. eines Monats
(d.h. periodisch)
erstmals am 15. November 1999
und letztmals am 15. März 2000. | 1000,00 Euro,

• Zusätzliche Zahlungen jeweils
am Ende eines bestimmten
Monats in folgender Höhe: |

- Oktober 1999 | 25,00 Euro,

- November 1999 | 47,50 Euro,

- Dezember 1999 | 42,50 Euro,

- Januar 2000 | 37,50 Euro,

- Februar 2000 | 32,50 Euro.

• Am 5. April 2000 | 5.031,67 Euro.

• Insgesamt | 10.216,67 Euro.


Daraus ergibt sich folgende Gleichung:

Mit dieser Gleichung lässt sich i durch schrittweise Annäherungen errechnen, die auf einem Taschenrechner programmiert werden können.

Das Ergebnis lautet i = 0,06174 ...; dieses Ergebnis wird auf 6,17 % gerundet.

(Text neue Fassung)

Anhang (zu § 6) Berechnung des effektiven Jahreszinses

I. Grundgleichung zur Darstellung der Gleichheit zwischen Kredit-Auszahlungsbeträgen einerseits und Rückzahlungen (Tilgung, Zinsen und Kosten) andererseits.

Die nachstehende Gleichung zur Ermittlung des effektiven Jahreszinses drückt auf jährlicher Basis die rechnerische Gleichheit zwischen der Summe der Gegenwartswerte der in Anspruch genommenen Kredit-Auszahlungsbeträge einerseits und der Summe der Gegenwartswerte der Rückzahlungen (Tilgung, Zinsen und Kosten) andererseits aus: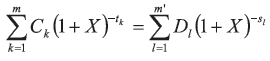

Hierbei ist

- X der effektive Jahreszins;

- m die laufende Nummer des letzten Kredit-Auszahlungsbetrags;

- k die laufende Nummer eines Kredit-Auszahlungsbetrags, wobei 1 ≤ k ≤ m;

- C_k die Höhe des Kredit-Auszahlungsbetrags mit der Nummer k;

- t_k der in Jahren oder Jahresbruchteilen ausgedrückte Zeitraum zwischen der ersten Darlehensvergabe und dem Zeitpunkt der einzelnen nachfolgenden in Anspruch genommenen Kredit-Auszahlungsbeträge, wobei t₁ = 0;

- m' die laufende Nummer der letzten Tilgungs-, Zins- oder Kostenzahlung;

- l die laufende Nummer einer Tilgungs-, Zins- oder Kostenzahlung;

- D_l der Betrag einer Tilgungs-, Zins- oder Kostenzahlung;

- s_l der in Jahren oder Jahresbruchteilen ausgedrückte Zeitraum zwischen dem Zeitpunkt der Inanspruchnahme des ersten Kredit-Auszahlungsbetrags und dem Zeitpunkt jeder einzelnen Tilgungs-, Zins- oder Kostenzahlung.

Anmerkungen:

a) Die von beiden Seiten zu unterschiedlichen Zeitpunkten gezahlten Beträge sind nicht notwendigerweise gleich groß und werden nicht notwendigerweise in gleichen Zeitabständen entrichtet.

b) Anfangszeitpunkt ist der Tag der Auszahlung des ersten Kreditbetrags.

c) Der Zeitraum zwischen diesen Zeitpunkten wird in Jahren oder Jahresbruchteilen ausgedrückt. Zugrunde gelegt werden für ein Jahr 365 Tage (bzw. für ein Schaltjahr 366 Tage), 52 Wochen oder zwölf Standardmonate. Ein Standardmonat hat 30,41666 Tage (d. h. 365/12), unabhängig davon, ob es sich um ein Schaltjahr handelt oder nicht.

d) Das Rechenergebnis wird auf eine Dezimalstelle genau angegeben. Ist die Ziffer der darauf folgenden Dezimalstelle größer als oder gleich 5, so erhöht sich die Ziffer der ersten Dezimalstelle um den Wert 1.

e) Mathematisch darstellen lässt sich diese Gleichung durch eine einzige Summation unter Verwendung des Faktors 'Ströme' (A_k), die entweder positiv oder negativ sind, je nachdem, ob sie für Auszahlungen oder für Rückzahlungen innerhalb der Perioden 1 bis k, ausgedrückt in Jahren, stehen: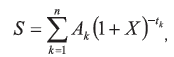

dabei ist S der Saldo der Gegenwartswerte aller Ströme, deren Wert gleich Null sein muss, damit die Gleichheit zwischen den Strömen gewahrt bleibt.

II. Zusätzliche Annahmen für die Berechnung des effektiven Jahreszinses

a) Kann der Kreditnehmer bestimmen, zu welchem Zeitpunkt er den Kredit in Anspruch nehmen will, gilt der gesamte Kredit als sofort in voller Höhe in Anspruch genommen.

b) Sieht der Kreditvertrag verschiedene Arten der Auszahlung mit unterschiedlichen Kosten oder Sollzinssätzen vor, gilt der gesamte Kredit als zu den höchsten Kosten und zum höchsten Sollzinssatz in Anspruch genommen, wie sie für die Art von Geschäften gelten, die bei dieser Kreditvertragsart am häufigsten vorkommt.

c) Kann der Kreditnehmer bestimmen, zu welchem Zeitpunkt er den Kredit in Anspruch nehmen will, sind jedoch je nach Art der Inanspruchnahme Beschränkungen in Bezug auf Betrag und Zeitraum vorgesehen, gilt der gesamte Kredit als zu dem frühesten vertraglich möglichen Zeitpunkt mit den entsprechenden Beschränkungen in Anspruch genommen.

d) Ist kein Zeitplan für die Tilgung festgelegt worden, ist anzunehmen, dass die Kreditlaufzeit ein Jahr beträgt und der Kredit in zwölf gleichen monatlich wiederkehrenden Raten zurückzuzahlen ist.

e) Ist ein Zeitplan für die Tilgung festgelegt worden, kann der Kreditnehmer jedoch die Höhe der einzelnen Tilgungsbeträge selbst bestimmen, ist anzunehmen, dass jeder Tilgungsbetrag dem niedrigsten im Kreditvertrag vorgesehenen Betrag entspricht.

f) Sieht der Kreditvertrag mehrere Termine für die Aus- oder Rückzahlung vor, gelten sowohl die Auszahlung als auch die Rückzahlung des Kredits als zu dem jeweils frühesten vertraglich möglichen Zeitpunkt erfolgt.

g) Ist keine Kreditobergrenze vereinbart, ist anzunehmen, dass der Betrag des gewährten Kredits 1.500 EUR beträgt.

h) Bei Überziehungsmöglichkeiten gilt der gesamte Kredit als in voller Höhe und für die gesamte Laufzeit des Kreditvertrags in Anspruch genommen; ist die Laufzeit des Kreditvertrags nicht bestimmt, ist sie mit drei Monaten anzunehmen.

i) Werden für einen begrenzten Zeitraum oder Betrag verschiedene Zinssätze und Kosten angeboten, so werden während der gesamten Laufzeit des Kreditvertrags als Zinssatz der höchste Zinssatz und als Kosten die höchsten Kosten angenommen.

j) Bei Verträgen, bei denen die Sollzinsbindung vor der für die Rückzahlung bestimmten Zeit endet und nach deren Ende ein neuer, veränderlicher Sollzinssatz vereinbart wird, der in regelmäßigen Abständen nach einem vereinbarten Index oder Referenzzinssatz angepasst wird, wird angenommen, dass der Sollzinssatz nach Ablauf der Sollzinsbindung dem Sollzinssatz entspricht, der sich aus dem Wert des vereinbarten Indexes oder Referenzzinssatzes zum Zeitpunkt der Berechnung des effektiven Jahreszinses ergibt.